Slide bài giảng Không gian vectơ

[Mr LNA]

Trích

Chương 3 - Bài 6 :






http://2.bp.blogspot.com/_SmhGHr5lVog/TJXKiJtu0YI/AAAAAAAAAyI/6jN9HH6hqy4/s1600/co+cau+to+chuc+cua+cong+ty.PNG Cơ cấu tổ chức của công ty

Giả sử F là một trường (có thể là trường số thực hay trường số phức). Các phần tử của F được gọi là số vô hướng. Một không gian vectơ V định nghĩa trên trường F là một tập hợp V không rỗng mà trên đó hai phép cộng vectơ và phép nhân với số vô hướng được định nghĩa sao cho cáctính chất cơ bản sau đây được thỏa mãn:

1. Phép cộng vectơ có tính kết hợp:
   
   
   Với mọi u, v, w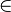 V, ta có u + (v + w) = (u + v) + w.
2. Phép cộng vectơ có tính giao hoán:
   
   
   Với mọi v, w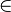 V, ta có v + w = w + v.
3. Phép cộng vectơ có phần tử trung hòa:
   
   
   Có một phần tử 0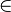 V, gọi là vectơ không, sao cho v + 0 = v với mọi v 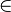V.
4. Phép cộng vectơ có phần tử đối:
   
   
   Với mọi v ∈ V, có một phần tử w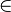 V, gọi là phần ngược của v, sao cho v + w = 0.
5. Phép nhân vô hướng phân phối với phép cộng vectơ:
   
   
   Với mọi a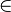 F và v, w 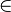V, ta có a (v + w) = av + aw.
6. Phép nhân vô hướng phân phối với phép cộng vô hướng:
   
   
   Với mọi a, b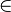 F và v 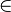V, ta có (a + b) v = av + bv.
7. Phép nhân vô hướng tương thích với phép nhân trong trường các số vô hướng:
   
   
   Với mọi a, b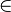 F và v 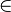V, ta có a (bv) = (ab) v.
8. Phần tử đơn vị của trường F có tính chất của phần tử đơn vị với phép nhân vô hướng:
   
   
   Với mọi v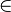 V, ta có 1 v = v, 1 kí hiệu đơn vị của phép nhân trong F.
   
   

[DOWNLOAD][/DOWNLOAD]
Định dạng PPT
File Size: 4.65 MB
Click here to Download