Trích từ tài liệu:
Bài 2 : Bài giảng định thức
Định nghĩa của định thức trong đại số tuyến tính liên quan đến khái niệm dấu của hoán vị.
Định thức của ma trận vuông cấp n là tổng đại số của n! (n giai thừa) số hạng, mỗi số hạng là tích của n phần tử lấy trên các hàng và các cột khác nhau của ma trận A, mỗi tích được nhân với phần tử dấu là +1 hoặc -1 theo phép thế tạo bởi các chỉ số hàng và chỉ số cột của các phần tử trong tích. Gọi Sn là nhóm các hoán vị của n phần tử 1,2,...,n ta có Công thức Leibniz)
Công thức Leibniz)
Khái niệm định thức xuất hiện đầu tiên gắn với việc giải hệ phương trình đại số tuyến tính có số phương trình bằng số ẩn. Hệ này có một nghiệm duy nhất khi và chỉ khi định thức của ma trận tương ứng với hệ phương trình này khác 0.
Ví dụ hệ hai phương trình tuyến tính hai ẩn:
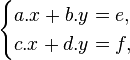 có các hệ số của các ẩn tạo thành ma trận vuông:
có các hệ số của các ẩn tạo thành ma trận vuông:
 định thức của nó là:
định thức của nó là:
det(A)=ad-bc .Nếu det(A) khác 0, hệ có nghiệm duy nhất
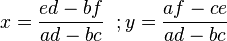 .Nếu det(A) = 0 hệ có thể có vô số nghiệm hoặc không có nghiệm nào.
.Nếu det(A) = 0 hệ có thể có vô số nghiệm hoặc không có nghiệm nào.
Nếu e = f = 0, hệ trên là một hệ phương trình tuyến tính thuần nhất, nó luôn có ít nhất một nghiệm tầm thường là x = 0 và y = 0. Khi đó hệ có nghiệm không tầm thường khi và chỉ khi định thức của hệ bằng không
[DOWNLOAD][/DOWNLOAD]
File Size: 1.38 MB
Định dạng PPT
Click here to Download
Bài 2 : Bài giảng định thức
Định nghĩa của định thức trong đại số tuyến tính liên quan đến khái niệm dấu của hoán vị.
Định thức của ma trận vuông cấp n là tổng đại số của n! (n giai thừa) số hạng, mỗi số hạng là tích của n phần tử lấy trên các hàng và các cột khác nhau của ma trận A, mỗi tích được nhân với phần tử dấu là +1 hoặc -1 theo phép thế tạo bởi các chỉ số hàng và chỉ số cột của các phần tử trong tích. Gọi Sn là nhóm các hoán vị của n phần tử 1,2,...,n ta có
Khái niệm định thức xuất hiện đầu tiên gắn với việc giải hệ phương trình đại số tuyến tính có số phương trình bằng số ẩn. Hệ này có một nghiệm duy nhất khi và chỉ khi định thức của ma trận tương ứng với hệ phương trình này khác 0.
Ví dụ hệ hai phương trình tuyến tính hai ẩn:
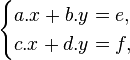

det(A)=ad-bc .Nếu det(A) khác 0, hệ có nghiệm duy nhất
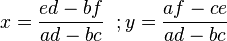
Nếu e = f = 0, hệ trên là một hệ phương trình tuyến tính thuần nhất, nó luôn có ít nhất một nghiệm tầm thường là x = 0 và y = 0. Khi đó hệ có nghiệm không tầm thường khi và chỉ khi định thức của hệ bằng không
[DOWNLOAD][/DOWNLOAD]
File Size: 1.38 MB
Định dạng PPT
Click here to Download
Bài tương tự bạn quan tâm
Slide tổng hợp toán cao cấp
- Thread starter saveyourtime1990
- Ngày bắt đầu
Slide bài giảng Ma trận
- Thread starter Mr LNA
- Ngày bắt đầu
Slide bài giảng Ma trận nghịch đảo
- Thread starter Mr LNA
- Ngày bắt đầu
Slide bài giảng Hạng ma trận
- Thread starter Mr LNA
- Ngày bắt đầu
Slide bài giảng Không gian vectơ
- Thread starter Mr LNA
- Ngày bắt đầu
Slide bài giảng Dạng toàn phương
- Thread starter Mr LNA
- Ngày bắt đầu



